Subdivision algorithms generate new meshes by dividing the faces and changing the locations of the vertices from the base polygonal meshes. It can preserve or smooth out the current shape of the meshes. The algorithms without changing the vertex locations exists, but they are less common. The main examples are Loop subdivision, Doo-Sabin subdivision, Catmull-Clark subdivision and 3 subdivision. In this project, we will see the Catmull-Clark and 3 subdivision and see the differences between them with examples implemented in C++ with the help of the OpenGL.
Where can subdivision algorithms be used?
It is primarily used in areas like visual effects, 3D modeling and computer animations. The achieved smoothing after the algorithms can speed up the process for creating a new smooth mesh from scratch. In the smoother versions of the meshes, because of the face count, the lighting and rendering will be much more realistic without losing the shapes look much. These differences in shading can be seen in the examples on the next sections.
Quad Meshes
For this project, we will see the Catmull-Clark algorithm which originally processes quad meshes only. However, the modern OpenGL only works with triangles in order to maintain performance because of the modern GPU architectures.
To solve this issue I created a Quad Mesh class which is operating on quads in the processing level, but turns quads into two triangles for the GPU. During the implementations I wanted to achieve a flat shading effect to show the faces during each iteration. For the quad meshes, to see this effect I give more than one normals which is not the case in default settings. For, example we can define a cube with 8 vertices and 12 triangles. In my implementation every vertex have different normals for the face they are part of. This way I can achieve the beatiful look in edges.
Catmull-Clark Subdivision
The Catmull-Clark algorithm creates surfaces recursiveley. The output mesh of the algorithm will only consist of quadritalerals which are not planar with their neigbours. The output will have a smoother look than the base mesh.
The algorithm simply defined with 4 different iterations on the elements of the base mesh which are vertices, edges and faces.
- In the beginning, for each face a face point created which is the center of the mass of the face.
- In the second iteration, for each edge an edge point is created which is the average of the neighbour faces face points and edges center point.
- In the next iteration, the vertex positions are updated according to following formula,
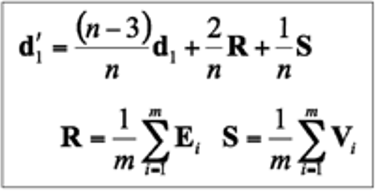
The d are the original vertices coordinates. R means the average of the neighbour edge points, and S means the average of the neighbour face points. The result will be a formulated weighted average of these points.
- In the final iteration, for each old face we define 4 new faces with the order like (old vertex, edge point, face point, edge point). For each old vertex we will have a new quad and we discard the old faces.
In the end we will left with a smoother new mesh which consists 3 times more quads than the base mesh.
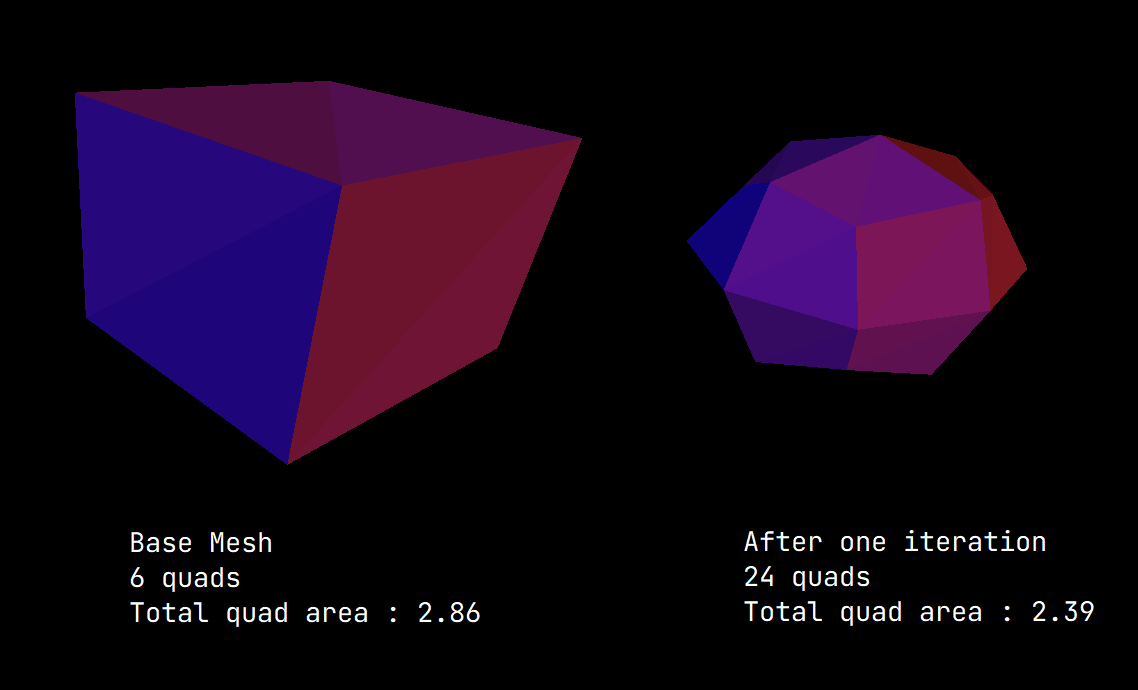
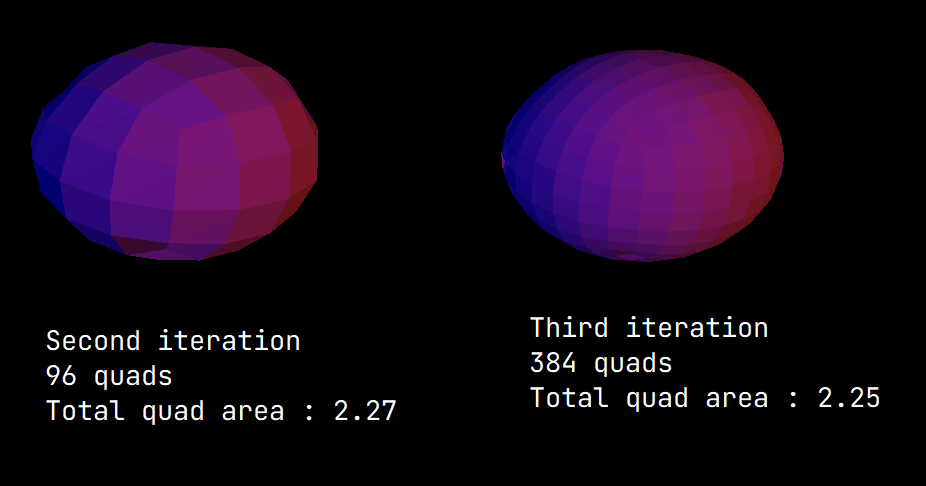
We can see the cube turns into a sphere like shape. However, it is not a perfect sphere because it can be experessed quadratic polynomials.
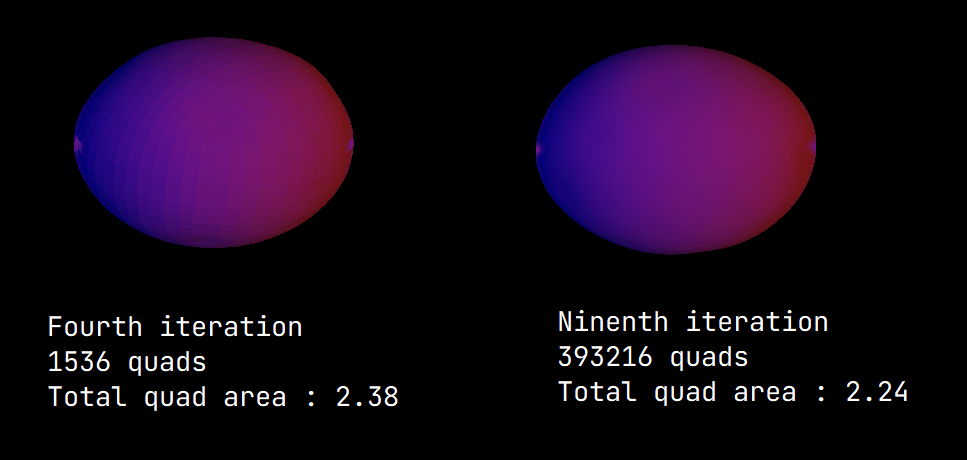
We can see the total area is steadily decreasing as the shape turns into a smoother one.
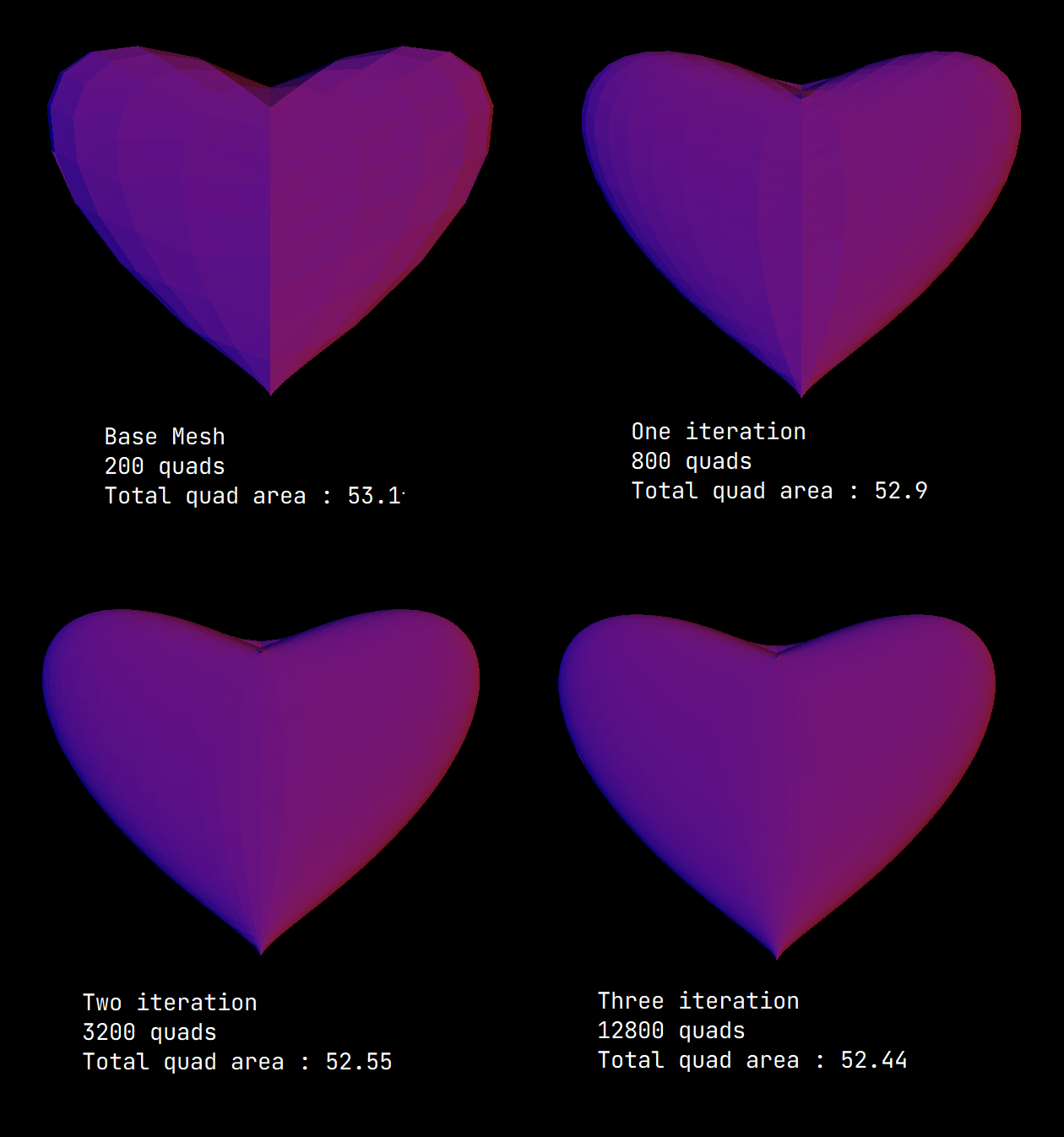
Problem with holes
While working on the algorithm, I notices some shapes are giving some weird results. For example the heart mesh is generating holes after the iterations. After some debugging I noticed that the given mesh points is not fully constructing a perfect two manifold mesh. This causes to algorithm thinking the the edges which are not supposed to be hole edges as holes.

To solve this problem I implemented a check whether the vertex is on a hole edge or not. If the vertex on the hole edge, I calculated its positions such that it doesn’t generate holes after the iterations.


However, as seen in the picture the hole edges can’t be smoothed because of the wrong neighbour informations after my solution. In the end I think not creating holes after iterations is generating more plausible meshes.
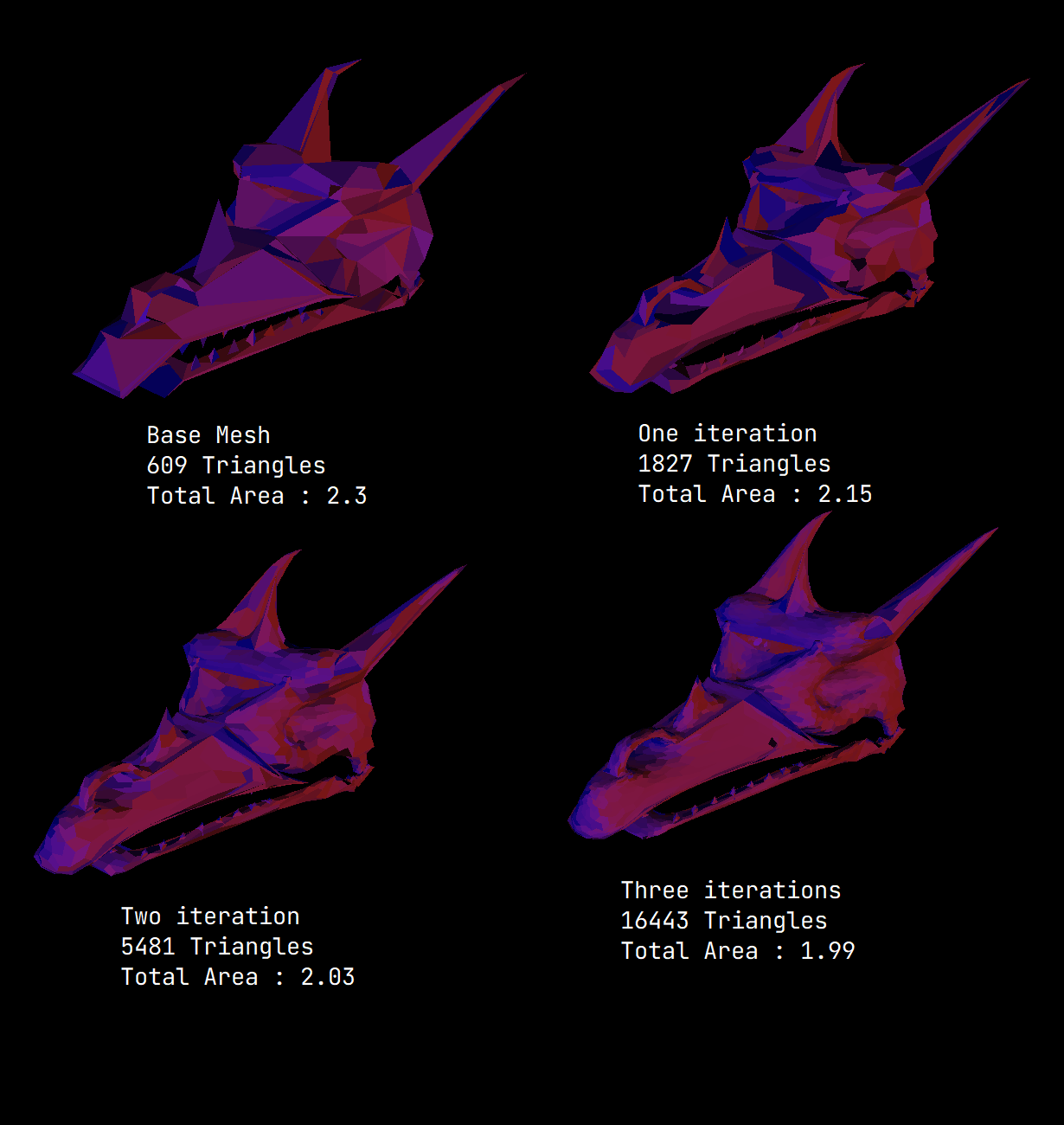
The next images are other examples with the Catmull-Clark algorithm.

Because of the complexity of the shape, the subdivision is not as visible as the other ones.
√3 Subdivision
The √3 subdivision is an alogrithm works with triangular meshes, the algorithm is a improved version of the 1-to-4 split operation which divides triangle faces to four triangle faces by adding new vertices to the middle of edges of the face. The improvements are the contiunity on the limit surfaces of the output being mostly C2 and handling sharp feature lines in a better way.
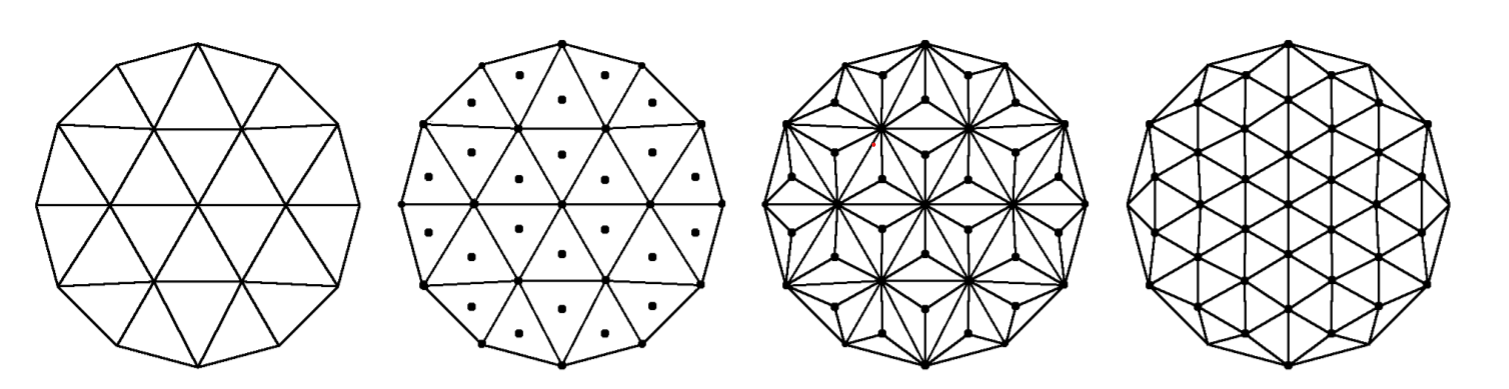
The algorithm is very intuitive and simple.
-
For every face, we will add a new vertex which is the center point of the triangle and connect the triangle points with the center point and create three new edges
-
Then we will relax (relocate the vertices according to their neighbours) the original vertices with a weighted formula
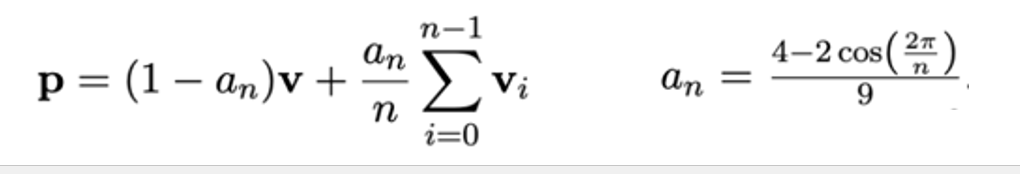
- In the end we will just flip the original edges in the base mesh which results in a smoother mesh with 2 times more triangles. The reason behind this number is that we create three faces from each face.
While implementing this algorithm the relaxation part is also created unwanted holes. I solved this via checking wheter the vertex is a in a edges which is hole edge. If the vertex is a hole vertex, I didn’t relax the positions of the vertex which solves the problem of unwanted holes during the iterations.

The decrease of total surface area exists in this algorithm too.

We can see from the iterations that holes are handled.
Final Notes
While implementing these algorithms, I used flat shading to show the change of the primitives. In every iteration which increases the face number, caused a more natural and realistic shading. The reason behind this is these algorithms smooths the shapes while keeping their look, with this way we can improve the shading by calculating the colors in a more detailed way. This property can be used in games, where for example if you approach a mesh, it can be subdivided to give the natural lightning feeling to it.
References
Leif Kobbelt. 2000. √3-subdivision. In Proceedings of the 27th annual conference on Computer graphics and interactive techniques (SIGGRAPH ‘00). ACM Press/Addison-Wesley Publishing Co., USA, 103–112. https://doi.org/10.1145/344779.344835
E. Catmull, J. Clark,Recursively generated B-spline surfaces on arbitrary topological meshes, Computer-Aided Design, Volume 10, Issue 6, 1978, Pages 350-355, ISSN 0010-4485, https://doi.org/10.1016/0010-4485(78)90110-0.
Yusuf Sahillioğlu, Lecture Slides from CENG589 Digital Geometry Processing, Middle East Technical University